供电的电路，其极性每周期改动一次，一般称为沟通(AC)电压和电流源。

  当电流流过导线或导体时，会在导线周围构成环形磁场，其强度与电流值相关。若使单根导线在停止磁场中移动或旋转，因为导体切开磁力线，导体内部会感应出电动势(EMF)。

  由此可见，电与磁之间有关联性，正如迈克尔·法拉第发现的电磁感应效应。这一根底原理被电机和发电机用来发生咱们日常运用的正弦沟通电。

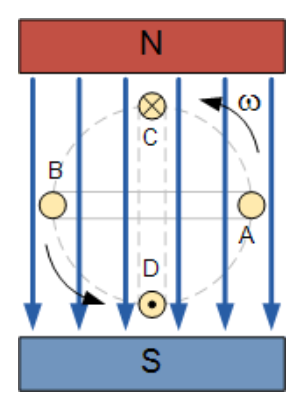
  在电磁感应教程中咱们说到，当单根导线切开永磁场的磁力线时，内部会感应出电动势。

  但是，当旋转导体在A、B两点方位与磁场平行移动时，没有切开任何磁力线，因而不会发生感应电动势。当导体在C、D两点方位与磁场笔直移动时，切开的磁力线数量最多，发生的感应电动势也最大。

  此外，导体在A、C两点之间(0-90°)以不同视点切开磁场时，感应电动势的巨细将介于零到最大值之间。因而，导体中的感应电动势巨细取决于导体与磁力线的夹角以及磁场强度。

  沟通发电机运用法拉第电磁感应原理，将旋转等机械能转化为电能——即正弦波形。简略发电机由一对永磁体组成，在南北极之间构成固定磁场。磁场内放置一个可绕固定轴旋转的矩形导线环，使其能以不同视点切开磁力线，如下图所示。

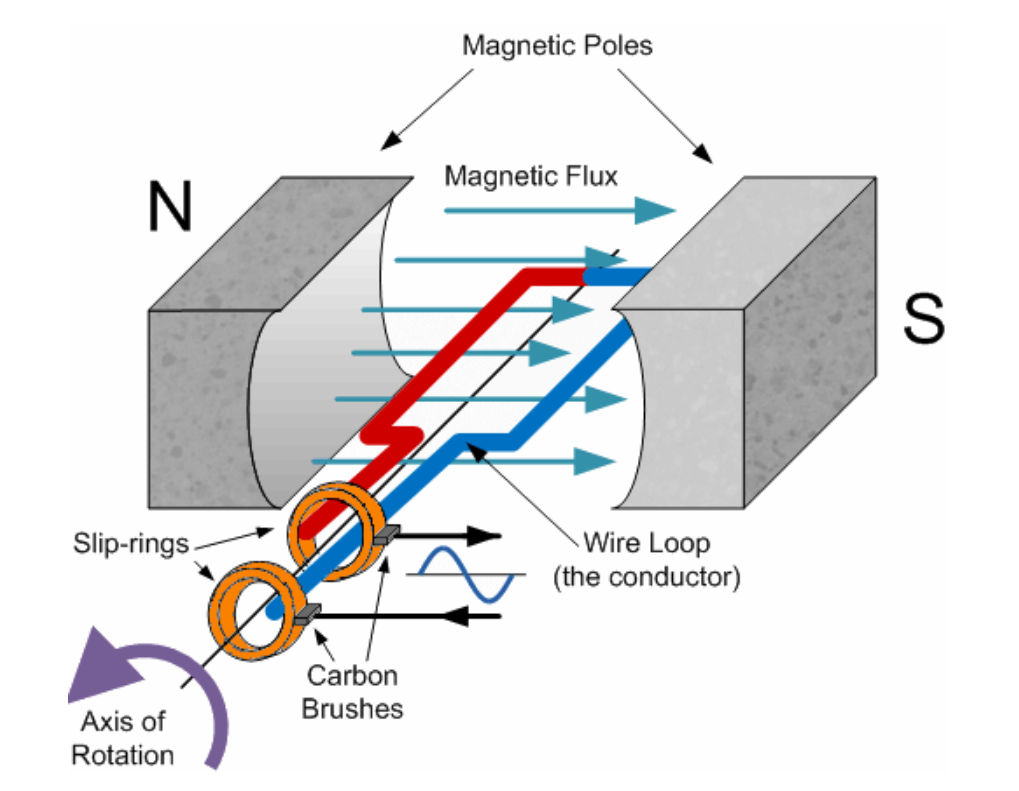
  当线圈沿笔直于磁场的中心轴逆时针旋转时，导线环以不同视点切开南北极之间的磁力线。恣意时刻线圈中的感应电动势巨细与导线环的旋转视点成正比。

  跟着导线环旋转，电子沿环向一个方向活动。当导线°点反向切开磁力线时，电子活动方向随即改动，然后改动感应电压的极性。

  由此可见，线°完好旋转，就发生一个完好周期的正弦波形。线圈在磁场中旋转时，经过碳刷和滑环将感应电流导出。

  咱们知道电源频率是指每秒呈现的周期数，单位为赫兹(Hz)。如上所示，线圈在包括南北极的磁场中每旋转一圈发生一个感应电动势周期，若坚持稳定转速，则每秒发生固定数量的周期，然后构成稳定频率。因而进步线圈转速将添加频率。故频率与转速成正比(ƒ∝Ν)，其间Ν=转/分钟(r.p.m)。

  此外，咱们简略的单线圈发电机仅有两个磁极(一北极一南极)，即一对磁极。若添加磁极数量至四个(两北极两南极)，则在相同转速下每转可发生两个周期。因而频率与磁极对数成正比(ƒ∝P)，其间P=磁极对数。

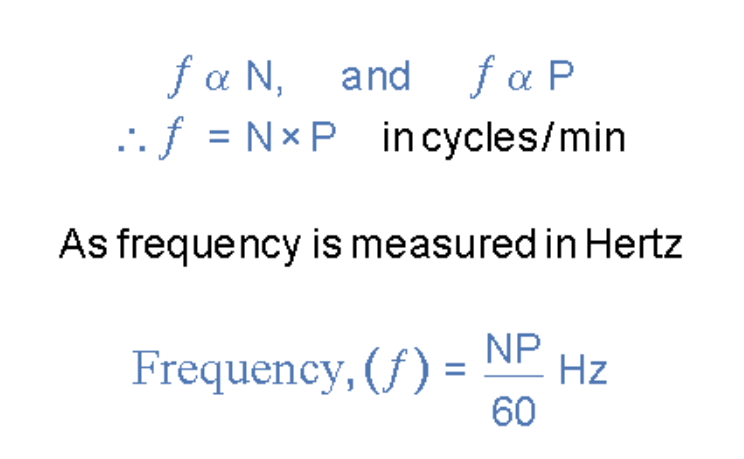
  线圈中恣意时刻的感应电动势取决于切开磁力线的速率，即与发电设备的旋转视点θ相关。因为沟通波形继续改动其幅值，每个瞬间的波形值都不相同。

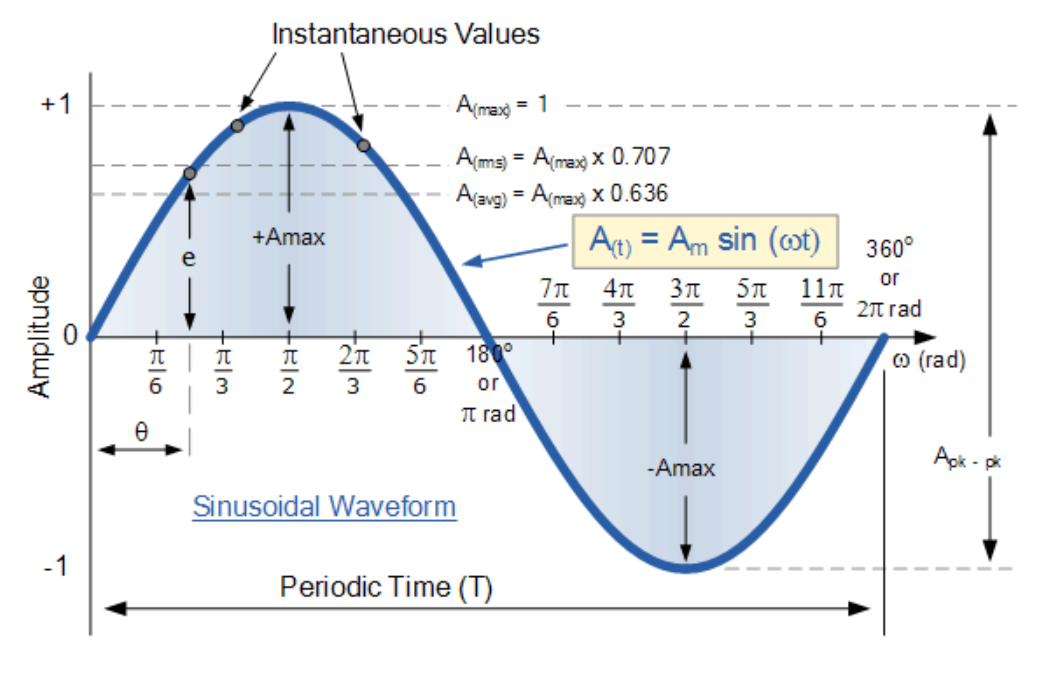
  例如，1ms时刻的值与1.2ms时刻的值就不同。这些值统称为瞬时值(Vi)。瞬时波形值及其方向随线圈在磁场中的方位而改动，如下图所示。

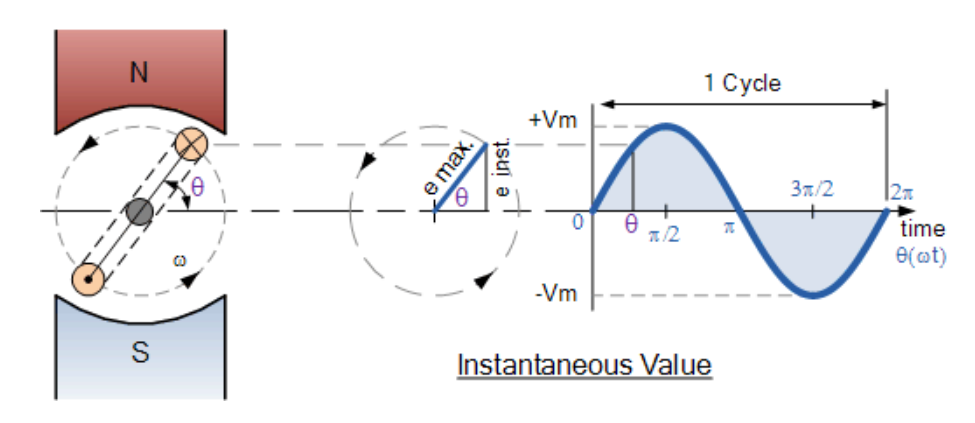
  正弦波形的瞬时值核算公式为：瞬时值=最大值×sinθ，通用公式标明为：

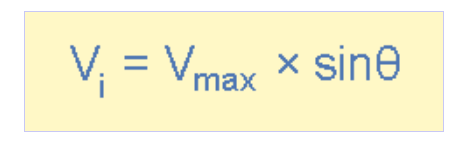
  其间Vmax为线圈中感应的最大电压，θ=ωt标明线圈随时刻改动的旋转视点。

  若已知波形峰值，经过上述公式可核算出波形各点的瞬时值。将这些值制作在坐标纸上，即可构建出正弦波形。

  为简化核算，咱们按每45°旋转角取一个瞬时值(共8个点)，并假定最大电压Vmax=100V。若选用更小距离(如每30°取12个点或每10°取36个点)制作，得到的正弦波形会更准确。

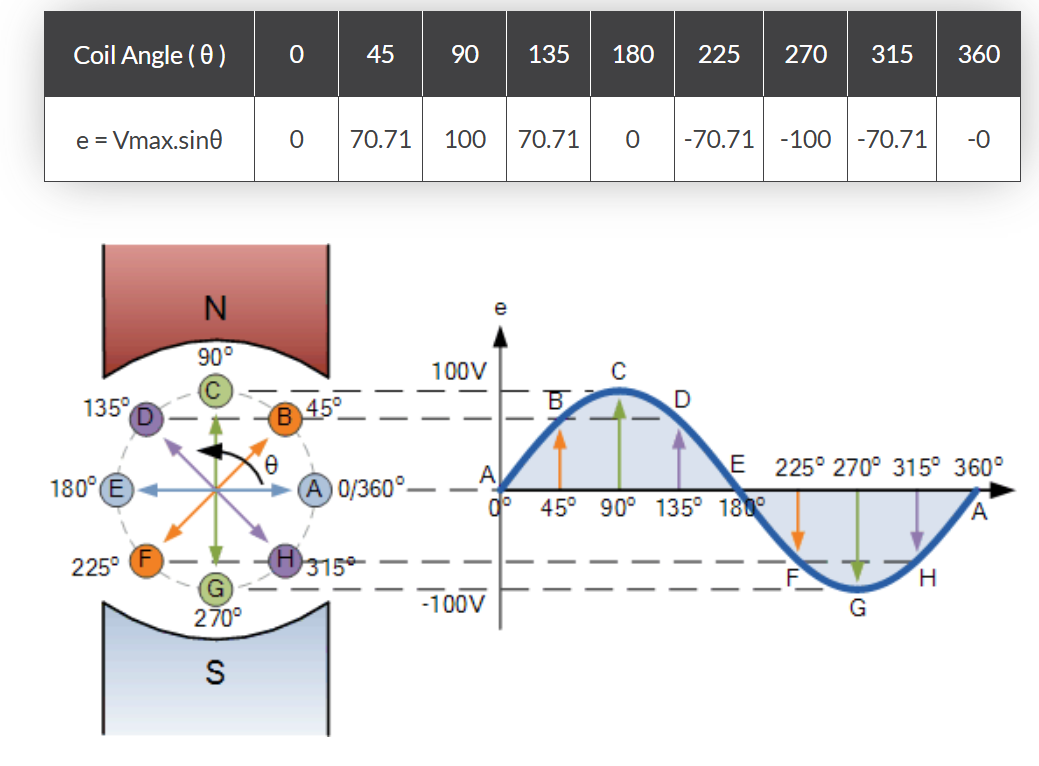
  经过将0°-360°旋转方位投影到波形纵坐标上取得各点。当导线°完好旋转时，即发生一个完好波形。

  从正弦波形图可见：当θ=0°、180°或360°时，因切开的磁力线最少，感应电动势为零；当θ=90°和270°时，因切开的磁力线最多，感应电动势到达峰值。

  因而正弦波形在90°处有正峰值，270°处有负峰值。B、D、F、H各点发生的电动势契合公式：e=Vmax.sinθ。

  这种由简略单环发电机发生的波形因其形状契合正弦函数而被称为正弦波。数学上标明为x(t)=Amax.sinθ。

  处理时域中的正弦波(尤其是电流相关正弦波)时，横轴单位可选用时刻、视点或弧度。电气工程中更常用弧度而非视点作为水平轴的视点量单位，例如ω=100rad/s或500rad/s。

  弧度(rad)的数学界说是：圆的象限弧长等于该圆半径(r)时的圆心角。因为圆周长为2π×半径，故360°圆周包括2π弧度。

  换言之，弧度是视点丈量单位，1弧度(r)对应的弧长在圆周上刚好呈现2π(约6.284)次。因而1弧度=360°/2π=57.3°。在电气工程中弧度运用十分遍及，需紧记以下公式：

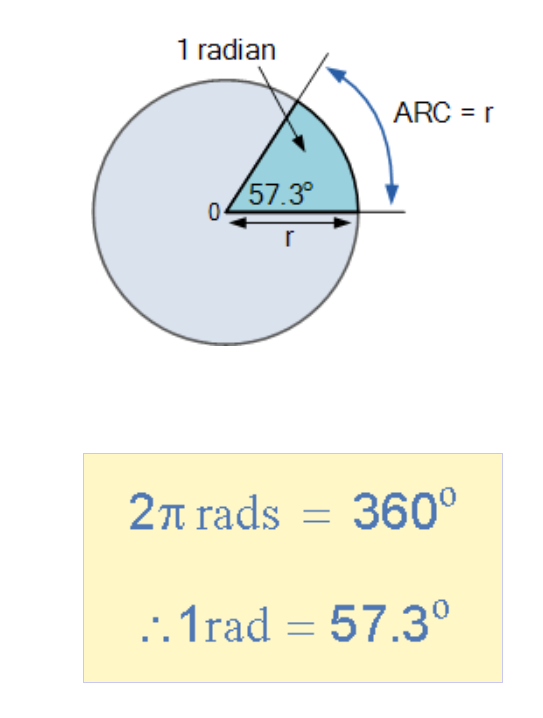
  运用弧度作为正弦波形的丈量单位时，360°完好周期对应2π弧度，半个正弦波形对应1π弧度(即π)。已知π≈3.142，因而正弦波形的视点与弧度转化联系为：

  发电机绕中心轴的旋转速度决议了正弦波的频率。当波形频率为ƒ赫兹(Hz)或周/秒时，波形还具有角频率ω(单位：弧度/秒)。正弦波的角速度公式为：

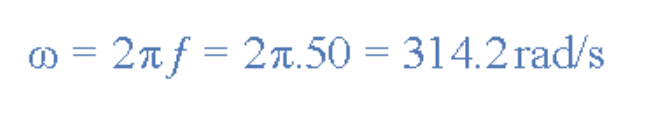
  至此咱们理解：发电机绕中心轴的旋转速度决议了正弦波的频率(即角速度ω)。一起还应知道，完结一整圈旋转所需时刻等于正弦波的周期(T)。

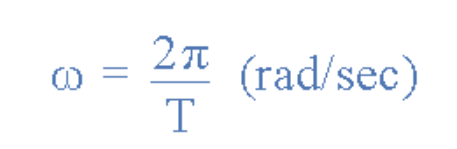
  该式标明：正弦波的周期越短，角速度有必要越大。同理，频率越高，角速度也越高。

  已知正弦波形界说为：Vm=169.8sin(377t)伏特。核算该波形的：

  注：t=6ms时的角速度以弧度标明。如需转化为视点值核算瞬时电压，转化公式为：

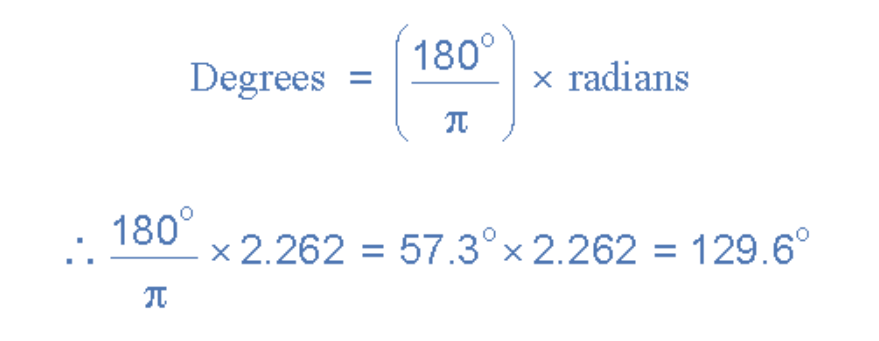
  鄙人一篇关于相位差的教程中，咱们将讨论两个同频率正弦波之间的联系，它们以不一起刻距离经过水平零轴。

• · 我变成一只狗
• · 圣安地列斯mod模组
• · 大国工程——西气东输：能源大动脉的传奇之路
• · 关于举办2024年全国作业作业技术竞赛——第二届“育轩科技杯”全国轿车修补服务作业技术竞赛的预告诉
• · 百万理想常州故事：本土供应链跻身“高端局”“核心局”